Задача о «Квантовых часах» (Кафедра 32 (Теоретической ядерной физики) МИФИ)¶
Построить численное решение временного уравнения Шредингера (одномерный случай)
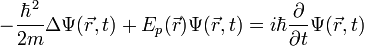
при условиях:
- Симметричный потенциал в виде двух одинаковых потенциальных ям. Простейший вариант - две прямоугольные ямы. Учтите, что ямки должны быть достаточно близко друг к другу (ширина барьера существенно меньше ширины ямок), чтобы вероятность туннелирования барьера между ними не была катастрофически мала. Какой именно вид потенциала Вы выберете - не принципиально, эффект должен проявляться на любом потенциале, подходящем под описание.
- Начальные условия - частица находится в одной из ямок. Можно задать волновую функцию, например распределением Гаусса, в пределах одной ямки. Можно пробовать и другие варианты, но учтите, что в начальном условии стоит избегать скачков волновой функции, или ее первой производной. Самое четкое проявления эффекта будет, если взять начальное условие как сумму основного и первого возбужденного состояний для выбранного потенциала. Разумеется, перед суммированием волновые функции необходимо отнормировать. Так как основное состояние - симметричное, а первое возбужденное - антисимметричное, их сумма будет преимущественно находиться в одной из ям (это утверждение справедливо если потенциал симметричен).
Что должно получиться:¶
Если задание выполнено правильно, Вы получите следующий результат: волновая функция будет со временем «перетекать» из одной ямки в другую и обратно, через одинаковые промежутки времени, подобно маятнику часов. Если начальное условие задано не как сумма двух собственных состояний, то в решении будут присутствовать разные дополнительные волны, но общая тенденция должна проявляться. Также допускается, что нормировка будет немного «гулять»- это может быть связано с неточностью численных вычислений. Ниже представлены результаты для различных потенциалов (синяя линия - квадрат модуля волновой функции, черная - потенциал) .
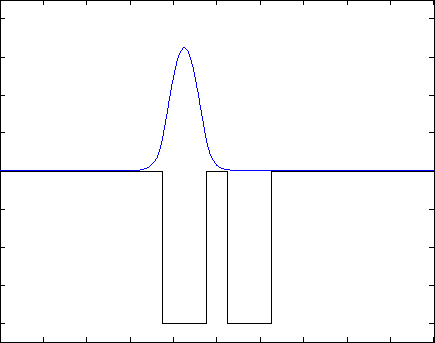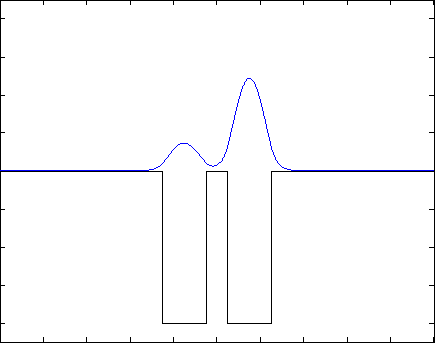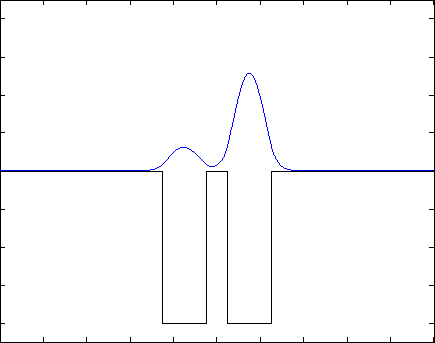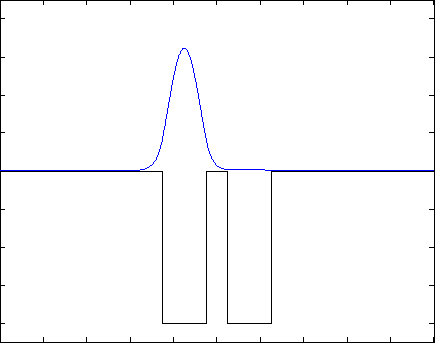
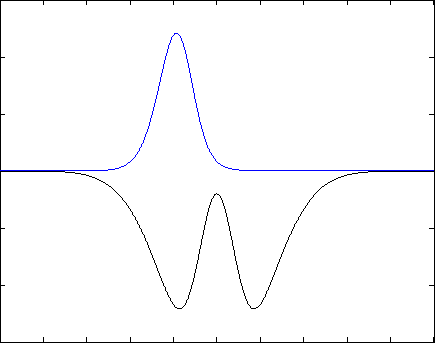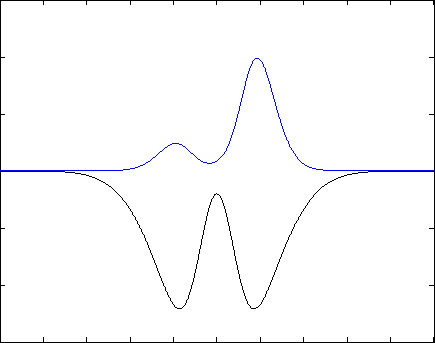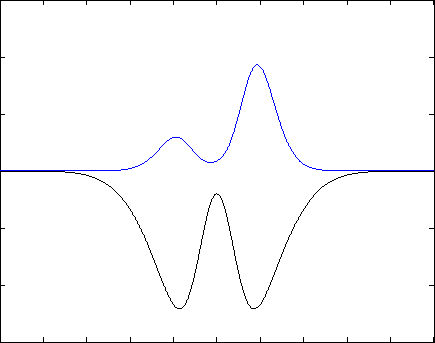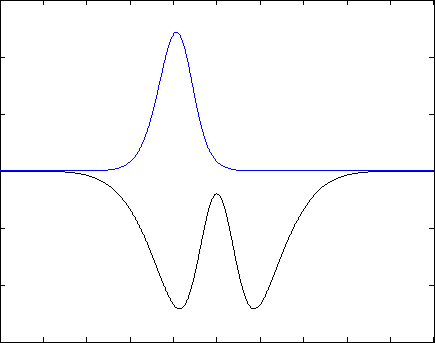
Указания к выполнению:¶
Явная схема неустойчива при решении временного уравнения Шредингера. Задачу можно попытаться выполнить по неявной схеме, но в этом случае Вы можете столкнуться с проблемой, что нормировка будет со временем уменьшаться. Это можно исправить, проводя перенормировку волновой функции после каждого шага по времени, но в некотором смысле это «жульничество». Для решения этой задачи лучше всего воспользоваться схемой Дюфорта-Франкеля (ромба). В отличии от простейшей явной разностной схемы, здесь на каждом шаге вместо средней точки по координате нужно взять полусумму следующего и предыдущего шагов по времени в этих точках. По своей сути эта схема напоминает явную, но вместо двух слоев по времени, в этой схеме задействовано три. Если обозначить за x и t индексы по координате и времени соответственно, то мы получим:
ΔΨ→[ Ψ(x+1,t) + Ψ(x-1,t) - Ψ(x,t-1) - Ψ(x,t+1) ] / h^2,
dΨ/dt→ [ Ψ(x,t+1) - Ψ(x,t-1) ] / ( 2 L ),
Ψ →[ Ψ(x,t+1) + Ψ(x,t-1) ] / 2,
где h - шаг по координате, L - шаг по времени. Такая схема всегда остается явной относительно Ψ(x,t+1) и является устойчивой при любых h и L. (см. Самарский А.А. Введение в теорию разностных схем). Произведите указанные выше замены во временном уравнении Шредингера и выразите Ψ(x,t+1). Как видно, одного начального условия не достаточно, чтобы начать пользоваться этой схемой, так-как нам нужно минимум 2 слоя по времени. Второй слой можно взять точно такой же, как и первый, но на практике это приводит к тому, что нормировка начинает довольно сильно «пульсировать». Намного более точное решение получится, если получить второй слой из первого по обычной явной схеме. Несмотря на то, что эта схема неустойчива, и со временем решение разваливается, один шаг по ней можно сделать без заметных последствий.
Дополнительные задания (необязательно):¶
- На примере случая, когда начальные условия являются суперпозицией основного и первого возбужденного состояний (считается что волновые функции и энергии известны) обоснуйте теоретически, откуда возникает эффект квантовых часов.
- Посмотрите, как происходит туннелирование/отражение волн от барьера (для этого необходимо придать волновой функции в начальных условиях импульс). Также можете рассмотреть случай, когда потенциальных ямок например пять.