Методы дискретизации ДУЧП

К сожалению, аналитическое решение уравнений математической физики возможно лишь для весьма ограниченного круга задач. В большинстве случаев решение дифференциальных уравнений в частных производных возможно только с использованием численных итерационных методов. Суть данных методов состоит в дискретизации дифференциальных уравнений, то есть представлении всех или части производных в виде приближенных выражений (конечных разностей или конечных элементов), что позволяет преобразовать дифференциальные уравнения в системы алгебраических уравнений. Для этого рассматриваемая область покрывается координатной сеткой, а все переменные заменяются сеточными функциями. Иными словами, значения переменных исследуются не для всего бесконечного множества точек области, а лишь для некоторого конечного подмножества. Причем при решении нестационарных задач помимо координатной сетки вводится сетка времени. Число алгебраических уравнений в полученной системе (размерность дискретной задачи) определяется произведением числа точек координатной сетки на количество независимых переменных в исходных дифференциальных уравнениях.

Выбор метода решения полученной системы алгебраических уравнений определяется ее размерностью и характером (линейный или нелинейный). Для решения систем линейных алгебраических уравнений (СЛАУ) широко используют метод исключения Гаусса, метод LU-разложения и др. Для решения систем нелинейных алгебраических уравнений и линейных систем больших размерностей используют итерационные методы Якоби, Зейделя, Ньютона-Рафсона и др.

Метод конечных разностей

Метод конечных разностей предполагает дискретизацию функций на некоторой сетке. Это означает, что рассматриваются значения в функции в дискретном наборе точек - узлах сетки, а производные заменяются конечными разностями - выражениями через используемые значения. Обычно выбираются сетки дискретизации совпадают с координатными сетками. Используют сетки совпадающие с системой координат. При таком выборе частные производные имеют известный вид. Для декартовой системы координат ячейки сетки представляют собой прямоугольники в случае двух измерений или параллелепипеды для трех измерений, а выражения для производных наиболее простой и привычный вид.

Правая разность:

\[\frac{\partial U}{\partial x} = \frac{U(x_0+h,y_0)-U(x_0,y_0)}{h}.\]

Левая разность:

\[\frac{\partial U}{\partial x} = \frac{U(x_0,y_0)-U(x_0-h,y_0)}{h}.\]

Центральная разность для первой и второй производных:

\[ \begin{align}\begin{aligned}\frac{\partial U}{\partial x} = \frac{U(x_0+h,y_0)-U(x_0-h,y_0)}{2h},\\\frac{\partial^2 U}{\partial x^2} = \frac{U(x_0+h,y_0)-2U(x_0,y_0)+U(x_0-h,y_0)}{h^2}\end{aligned}\end{align} \]

Аналогично строятся смешанные производные и производные высших порядков.

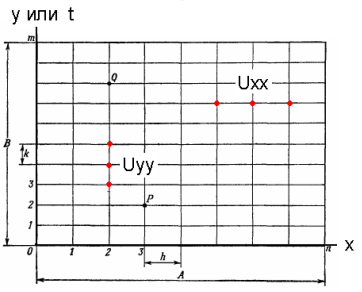
Пример сетки для дискретизации ДУЧП

Для эллиптических уравнений выбирается сетка по пространственным координатам, а если уравнение параболическое или гиперболическое, то и по времени (см. рисунок). ДУЧП после такой замены превращается в систему алгебраических уравнений, решение которой проводится стандартными методами. Размер системы уравнений определяется плотностью сетки, а увеличение точности достигается уменьшением шага разбиения.

Для однородного эллиптического уравнения \(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} = 0\) разностное уравнение имеет вид: \(\lambda^2 u_{i+1,j} +\lambda^2 u_{i-1,j} + u_{i,j+1} + u_{i,j-1} -2(1+\lambda^2) u_{i,j} =0\), где отношение шагов разбиения по разным координатам обозначено \(\lambda = k/h\).

Для удобства представления разностные схемы уравнений записывают на сетке, в узлах которой отмечают весовые коэффициенты, которые нужно взять, чтобы линейная комбинация значений давала ноль. Для эллиптического уравнения схема представлена на рисунке.

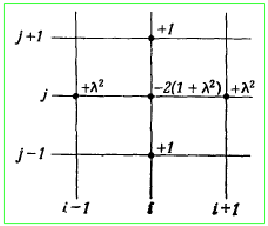
Графическое представление разностной схемы для эллиптического уравнения

Решение полученной системы уравнений может быть проведено методом последовательных приближений. Для этого задается начальное приближение во всех узлах сетки, а затем значания в каждом узле пересчитываются по схеме приведенной выше. Для такого метода выполнено условие сходимости, поэтому в результате получаем искомое решение.

Для решения гиперболического уравнения необходимо задать граничные условия для всех моментов времени: \(u(t)|_\Gamma\) и начальные условия для значения функции и ее производной: \(u(\vec{r},0), \left. \frac{\partial u(\vec{r},t)}{\partial t} \right|_{t=0}\).

Разностное гиперболическое уравнение можно записать в виде: \(\lambda^2 u_{i+1,j} +\lambda^2 u_{i-1,j} - u_{i,j+1} - u_{i,j-1} + 2(1-\lambda^2) u_{i,j} =0\), где \(\lambda = k/h\). Графическая схема полученного метода приведена на рисунке.

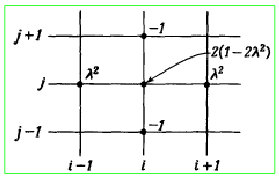
Графическое представление разностной схемы для гиперболического уравнения

Начальные условия при t = 0 задают значения функции на нижнем слое точек (j = 1), а ее производные позволяют вычислить значения функции на втором слое точек (j=2). Граничные условия обеспечивают полноту информации для каждого слоя. Решение данной разностной схемы может быть выполнено в явном виде. Достаточно выразить значение функции на следующем слое через известные значения на предыдущих:

\(u_{i,j+1} = \lambda^2 u_{i+1,j} +\lambda^2 u_{i-1,j} - u_{i,j-1} + 2(1-\lambda^2) u_{i,j}\), где \(\lambda = k/h\).

Для данной схемы условием устойчивости является \(k<h\), т.е. шаг по координате должен быть больше, чем шаг по времени. Это не совсем удобно, т.к. не позволяет вести интегрирование с большим шагом.

Для параболических уравнений также как и для гиперболических задаются начальные и граничные условия. Из-за первого прорядка таких уравнений по времени в качестве начальных условий достаточно задать только значения функции \(u(\vec{r},0)\).

Простейшее разностная схема для параболического уравнения: \(u_{i,j+1} - \lambda u_{i+1,j} -\lambda u_{i-1,j} - (1-2\lambda) u_{i,j}=0\), где \(\lambda = k/h\).

Его графическая схема показана на рисунке.

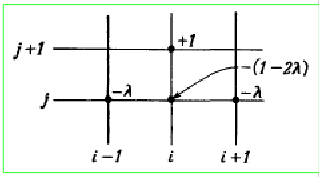
Графическое представление явной разностной схемы для параболического уравнения

Явная схема устойчива при \(k<h^2/2\) , т.е. шаг по времени меньше, чем квадрат сетки по координате. Это очень сильное условие, которое делает явную схему не работоспособной. Неустойчивость решения вызвана слабой связью между соседними точками на следующем слое. При потере устойчивости возникает знакопеременное решение с близкими по модулю значениями. Это укладывается в данную разностную схему т.к. значения функции в соседних точках суммируются.

Поэтому для параболического уравнения обычно используются неявные схемы вычислений.

Простая неявная схема, которая устойчива при всех параметрах: \(-u_{i,j} - \lambda u_{i+1,j+1} -\lambda u_{i-1,j+1} + (1+2\lambda) u_{i,j+1} = 0\).

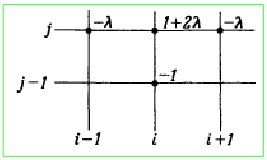
Графическое представление неявной разностной схемы для параболического уравнения

Метод Кранка – Николса, который тоже устойчив при всех параметрах используют лучшую аппроксимацию производных:

\(\frac{\lambda}{2} (u_{i-1,j}+u_{i+1,j}+u_{i-1,j+1}+u_{i+1,j+1}) - (\lambda+1)u_{i,j+1} - (\lambda-1)u_{i,j} =0\).

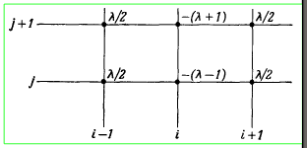
Графическое представление метода Кранка-Николса для параболического уравнения

Неявные схемы вычислений приводят к необходимости решать на каждом шаге систему линейных уравнений типа \(a u_{i-1,j+1} + b u_{i,j+1} + c u_{i+1,j+1} = d\), но большой плюс состоит в том, что эта системы трехдиагональна и хорошо решается методом прогонки.

Метод конечных элементов

предполагает дискретизацию дифференциальных уравнений на нерегулярных, так называемых триангулярных координатных сетках, то есть на сетках, элементарные ячейки которых представляют собой треугольники для двух измерений или призмы (тетраэдры) для трех измерений. При этом уравнения (производные) приписываются не узлам сетки, а ее элементам.