Вариационные методы

Краевую задачу для дифференциального уравнения можно переписать в эквивалентном интегральном виде. Например эллиплическое уравнение

\[ \begin{align}\begin{aligned}div[k(x)grad(U)]-\rho(x)u(x)=-f(x), x \in G\\U|_{\Gamma} = \mu (x)\end{aligned}\end{align} \]

эквивалентно вариационной задаче

\[\int_G [k(x) (grad(U))^2 +\rho(x)u^2(x)-2f(x)u(x)] = min, U|_{\Gamma} = \mu (x).\]

При поиске ее решения можно использовать разложения по любому набору функций:

\[U(x) \approx \phi_0(x)+\sum_{i=1}^n c_i \phi_i(x),\]

где \(\phi_0\) удовлетворяет граничному условию, а все \(\phi_i\) равны нулю на границе.

При этом задача минимизации сводится к

\[\int_G \left[ \sum_{r=1}^n \sum_{l=1}^n c_r c_l (k \cdot grad \psi_r grad \psi_l + \rho \psi_r \psi_l) - 2f \sum_{r=1}^n c_r \psi_r \right] dx = min,\]

что эквивалентно системе из n линейных уравненй относительно \(c_l\):

\[\sum_{l=1}^n c_l \int_G (k \cdot grad \psi_r grad \psi_l + \rho \psi_r \psi_l) dx = \int_G f \psi_r dx, r = 1...n,\]

которая легко решается.

Основная трудность прииспользовании вариационного метода заключается выборе базиса, подходящего для конкретной задачи. Базис должен представлять решение по-возможности малым числом функций (т.е. быть изначально «похожим» на решение), и интегралы, входящие в приведенные выше выражения, дожны легко считаться.

Одним из удачных решений является использования базисов с компактным носителем, наиболее простым их которых является базис, используемый в методе Рица. В нем используются непрерывные кусочно-линейные функции, каждая из которых отлична от нуля только в небольшой области вблизи узла сетки разбиения области решения уравнения. Пример используемых функций для одномерного случая приведен на рисунке.

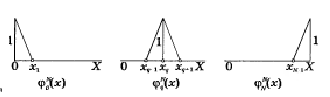
Базисный набор для метода Рица в случае одного измерения

Каждая функция при этом легко определяется:

\[\begin{split}\psi_q(x) = \left\{ \begin{array}{lr} \frac{x-x_{q-1}}{x_q-x_{q+1}} & : x_{q-1}<x<x_q \\ \frac{x_{q+1}-x}{x_{q+1}-x_q} & : x_q<x<x_{q+1} \\ 0 & : x<x_{q-1}, x>x_{q+1} \end{array} \right. .\end{split}\]

Полная функция - линейная комбинация базисных: \(u(x) = \sum_{q=1}^n c_q \psi_q(x)\). Ее производная находится тривиально: \(u'(x) = c_q \psi'_q(x)+c_{q+1} \psi'_{q+1}(x), x_q<x<x_{q+1}\), а вторая производная равна нулю.

Применение вариационного принципа для указанного базиса приводит к системе линейных уравнений с ленточной матрицей, которая эффективно решается методом прогонки. Получаемый набор коэффициентов - значения искомой функции в узлах сетки разбиения.

Для двух и трехмерного случая базис строится аналогично. Сначала выбирается треугольная сетка (проводится триангуляция области G). Один из способов триангуляции в случае двух переменных показан на рисунке.

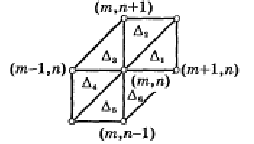
Триангуляционная сетка для метода рица в случае двух измерений

Затем строится базис:

\[\begin{split}\psi_{ij}(x,y) = \left\{ \begin{array}{lr} 1 & : (x,y) = (i*h, j*h) \\ 0 & : (x,y) \ne (i*h, j*h) \end{array} \right. ;\end{split}\]

строится искомая функция: \(U(x,y)=\sum_{i,j} c_{ij} \psi_{ij}(x,y)\);

и решается уравнение:

\[\sum_{i,j} c_{i,j} \int_G \left( \frac{\partial \psi_{ij}}{\partial x} \frac{\partial \psi_{mn}}{\partial x} + \frac{\partial \psi_{ij}}{\partial y} \frac{\partial \psi_{mn}}{\partial y}\right) dxdy = \int_G f(x,y) \psi_{mn}(x,y) dxdy .\]

Все выражения, входящие в уравнения просто вычисляются, полученная алгебраическая система имеет разреженную матрицу и может быть эффективно решена на компьютере.