Задания¶
- Задача 1 (Карпов А.)
Решите эллиптическое уравнение \(U_{xx} + U_{yy}=0\), используя соотношения:
Граничные условия и размер сетки изображены на рисунке. Итерации производить до тех пор, пока разности между последовательными значениями не будут 0,001.
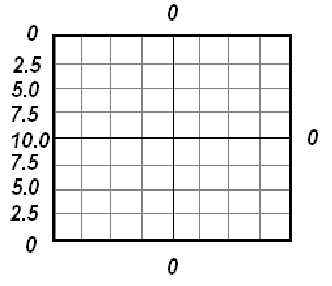
- Задача 2 (Чалов Д.)
Дана проводящая рамка 10 х 10 см, имеющая потенциал 10 В. В центре рамки расположен проводящий заземленный (потенциал 0 В) равносторонний треугольник со стороной а = 3 см.
- Найти потенциал поля в каждой точке области, ограниченной рамкой. Для этого решить уравнение Лапласа на сетке 200 x 200. Итерации производить до тех пор пока разности между последовательными значениями не будут меньше \(10^{-6}\).
- Рассчитать плотность зарядов на рамке.
- Построить графики.
- Задача 3 (Абрамова А.)
Внутри квадратной проводящей рамки со стороной а = 1 м находится заряженный до потенциала 15 В проводник в виде диска с радиусом r = 1 см.
- Найти потенциал поля в каждой точке области, ограниченной рамкой. Для этого решить уравнение Лапласа на сетке 400 x 400. Итерации производить до тех пор пока разности между последовательными значениями не будут меньше \(10^{-6}\).
- Рассчитать плотность зарядов на рамке.
- Построить графики.
- Задача 4 (Чупин И.)
Решите параболическое уравнение \(U_{xx} = U_t\) на отрезке \(x = [0, 1]\) для \(t_{max} = 200\).
Граничные условия: \(U(x = 0) = 100\), \(U(x = 1)=200\).
Начальные условия: \(U(x, t = 0)=100(1 - 2x)\), для \(x < 0.5\), \(U(x, t = 0)=200(2x - 1)\), для \(x > 0.5\).
- Для решения выбрать сетку по x, содержащую 100 узлов. Шаг по t подберите самостоятельно.
- Выполните решение явным и неявным методами. Сравните результаты.
- Задача 5 (Белов К.)
Решите параболическое уравнение \(U_{xx} = U_t\) на отрезке \(x = [0, 1]\) для \(t_{max} = 200\).
Начальные условия выберите в виде \(U(x, t = 0) = sin(2\pi x)\).
Граничные условия \(U_x(x = 0) = 0\), \(U_x (x = 1) = 0\).
- Для решения выбрать сетку по x, содержащую 100 узлов. Шаг по t подберите самостоятельно.
- Выполните решение явным и неявным методами. Сравните результаты.
- Задача 6 (Гавриляк А.)
Решите волновое уравнение: \(\frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x} \left(v \frac{\partial u}{\partial x}\right)\) на отрезке \(x = [-1, 1]\) для начального распределения \(u(x, t=0) = cos^2(5\pi x)\) для \(x = [-0.1, 0.1]\), и \(u = 0\) для остальных х. Для решения выбрать сетку по x, содержащую 200 (или 201) узлов. Шаг по t подберите самостоятельно. Считайте, что \(u(x = -1) = u(x = 1) = 0\).
- Решить уравнение для постоянной скорости распространения волны \(v = 0.04\) и \(t_{max} = 100\).
- Решить уравнение для волны с \(v = 0.04|x|^{0.5}\) и \(t_{max} = 150\).