Задания по диференциальным уравнениям¶
- Решите уравнение Шредингера с потенциалом V(x).
\(\psi''(x)+(E-V(x))\psi(x)=0\), \(V(x) = -20*\frac{1-0,8*cos(0,41*(x-0,01))}{cosh(0,42x)}\) найдите 6 нижних уровней энергии с точностью \(10^{-11}\)
- Решите уравнение Шредингера с потенциалом V(x).
\(\psi''(x)+(E-V(x))\psi(x)=0\), \(V(x) = (-2,1+0,11x)(tanh(5+x)+tanh(5-x))\) найдите 4 нижних уровней энергии с точностью \(10^{-11}\)
- Решите радиальное уравнение Шредингера с потенциалом V(r).
\(\psi''(r)+(E-V(r))\psi(r)=0\), \(V(r) = -\frac{1}{r} + \frac{2}{r^2} + \frac{0,001}{r^4}\) найдите 6 нижних уровней энергии с точностью \(10^{-11}\)
- Циклотронный резонанс
В начале координат покоится электрон. По оси Z направлено однородное магнитное поле B = 0,1 Т. В момент t = 0 включается электрическое поле E = A*sin(2πf t), направленное по оси X; A = 1000 В/м, частота f вводимый параметр.
Задание:
- Нарисовать траекторию движения r(t) в плоскости X, Y и график кинетической энергии W(t) электрона за время t = 3,57 нсек.
- Построить график кинетической энергии W электрона, которую он набирает за время t = 3,57 нсек, в зависимости от частоты f электрического поля. Частоту f удобно выражать в ГГц, энергию W – в эВ. Интересующий диапазон частот f = [2,5 , 3,1] ГГц. Какую максимальную энергию Wmax набирает электрон? При какой частоте fmax это происходит?
- Какую максимальную энергию Wmax электрона (за произвольное время) можно получить при f = 2,52 ГГц? Используя график траектории электрона, объяснить качественно получаемый результат.
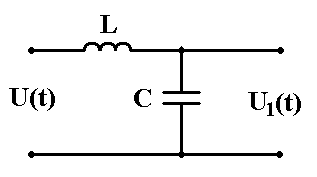
- Фильтр электрического сигнала
Простейший фильтр электрического сигнала показан на рисунке. В качестве элементов обычно выступают сопротивления, конденсаторы или катушки индуктивности. В данном случае индуктивность и сопротивление. На вход подается напряжение, зависящее от времени U(t), а на выходе получается напряжение U1(t).
Задание:
- Запишите систему уравнений, позволяющую найти напряжение U1(t) при известном U(t). Считайте сопротивление нагрузки равным R.
- Приведите полученную систему к стандартному виду.
- Решите систему для L=1мГн, C=10мкФ, U(t)=t.
- Решите задачу в случае, если U(t) - периодическая функция с периодом 1мс. Форма сигнала - синусоидальный сигнал, прямоугольные импульсы, треугольные импульсы.
- Фильтр электрического сигнала 2
Решите предыдущую задачу с переставленными L и С элементами.
- Маятник Капицы
Познакомьтесь с описанием маятника Капицы, данном в разделе Маятник Капицы.
Задание:
- Напишите программу, вычисляющую положение маятника в процессе движения.
- Визуализируйте движение маятника с одновременным построением траектории на фазовой плоскости.
- Задайте частоту внешней силы в 10 раз больже частоты собственных колебаний.
- Попробуйте установить амплитуду выдуждающие силы больше \(\sqrt{2gl/ \gamma^2}\).
- Что происходит, если маятник запускать из положения близкого к 180 градусам?
- Упругое соударение
- Цилиндр массы M = 1 кг и длиной 5 см висит на длинной пружине жесткости k = 50 Н*м. Через отверстие в верхнем
- основании внутрь цилиндра падает тело массы m = 0,5 кг с начальной скоростью v = 3 м/с. Считая, что движение происходит только вдоль вертикальной прямой, ответьте на вопросы.
Задание:
- Предложите модель упругого взаимодействия тела и цилиндра с характерным расстоянием ~ 1 мм.
- Напишите программу, вычисляющую положение тел в процессе движения.
- Проверьте, что сохраняется механическая энергия системы.
- Постройте для тела и цилиндра графики зависимости координаты и скорости от времени.
- Можно ли подобрать размеры элементов системы, чтобы через некоторое время они двигались как единое целое?
- Столкновение частиц
Две одинаковые частицы движутся с одинаковыми скоростями издалека навстречу друг другу. Частицы взаимодействуют с парным потенциалом \(\phi(r) = \epsilon \left( (r/r_0)^{-12} - (r/r_0)^{-6} \right)\).
Задание:
- Преобразуйте задачу к задаче о движении одной частицы относительно центра масс.
- Напишите программу, вычисляющую траекторию движения частицы относительно центра масс. Определите в программе угол рассеяния. Можете воспользоваться информацией раздела Движение пары взаимодействующих частиц.
- Найдите зависимость угла рассеяния (с учетом знака) от прицельного параметра для некоторой небольшой начальной скорости. Постройте график. Укажите точки в которых есть особенности.
- Вблизи особенности найдите зависимость времени столкновения от скорости частицы.
- Определите параметры, чтобы время столкновения было максимально.