Решение дифференциальных уравнений¶
Обыкновенные дифференциальные уравнения(ОДУ)¶
Обыкновенные дифференциальные уравнения (ОДУ) или системы обыкновенных дифференциальных уравнений записывают в виде: \(\frac{d}{dt}x_i(t)=f_i(x_1,x_2,...x_n,t)\) для всех i от 0 до n или \(\frac{d}{dt}\vec{x}(t)=\vec{f}(\vec{x},t)\). Уравнения высших порядков легко переписываются в таком виде после замены переменных. Результат решения системы ДУ может быть получен если дополнительно заданы n условий вида \(x_i(t_i)=C_i\). В соответствии с заданными дополнительными условиями различают два типа задач с разным смыслом: задачу Коши и краевую задачу. Для задачи Коши все дополнительные условия заданы для одного состояния системы, для одной точки \(t\), поэтому ее физическим смыслом является ответ на вопрос: «Как будет двигаться известная система в будущем (или в прошлом)?» Для краевой задачи дополнительные условия заданы для разных состояний системы, разных точек \(t_i\). Ее решение дает ответ на вопрос: «Как привести систему в нужное состояние?» Обычно решение ОДУ ищется через решение задачи Коши, т.к. она является более простой.
Решение задачи Коши¶
Задача Коши для ОДУ решается «шаговыми» методами - последовательным восстановлением функции \(\vec{x}(t)\) по ее значению в начальной точке \(\vec{x}(0)\) и известной производной (функции \(\vec{f}(\vec{x},t)\)). Простейшим методом является метод Эйлера: \(\vec{x}_{m+1}=\vec{x}_m+dt*\vec{f}(\vec{x}_m,t)\), где dt – шаг по времени.

Один шаг по фрмуле Эйлера
В методе Эйлера восстанавливается ломаная линия, как показано на рисунке. Ошибка решения метода Эйлера на каждом шаге порядка dt, поэтому решение методом Эйлера довольно быстро уходить от истиннй функции.
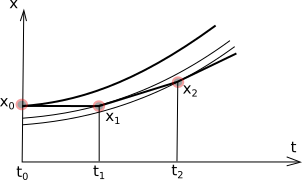
Отклонение решения от истинного
Можно повысить порядок метода Эйлера путем небольшого уточнения. Дело в том, что производную нужно считать не в той точке из которой мы делаем шаг, а в точке dt/2 (модифицированный метод Эйлера) или брать среднюю производную между начальной и конечной точками (исправленный метод Эйлера).
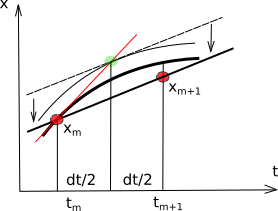
Модифицированный метод Эйлера: \(\vec{k}_1=\vec{f}(\vec{x}_m,t)\); \(\vec{k}_2=\vec{f}(\vec{x}_m+\vec{k}_1*dt/2,t+dt/2)\); \(\vec{x}_{m+1}=\vec{x}_m + dt*\vec{k}_2\)
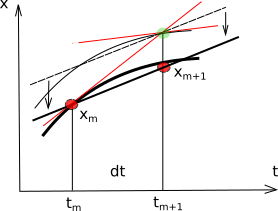
Исправленный метод Эйлера: \(\vec{k}_1=\vec{f}(\vec{x}_m,t)\); \(\vec{k}_2=\vec{f}(\vec{x}_m+\vec{k}_1*dt,t+dt)\); \(\vec{x}_{m+1}=\vec{x}_m + dt*(\vec{k}_1+\vec{k}_2)/2\)
Все «шаговые» методы носят названия методов Рунге-Кутта. Исправленный и модифицированный методы Эйлера относятся к методам Рунге - Кутты второго порядка точности.
Методы Рунге-Кутты третьего и высших порядков строятся аналогично. Например схема метода четвертого порядка задается уравнениями: \(\vec{k}_1=\vec{f}(\vec{x}_m,t)\); \(\vec{k}_2=\vec{f}(\vec{x}_m+\vec{k}_1*dt/2,t+dt/2)\); \(\vec{k}_3=\vec{f}(\vec{x}_m+\vec{k}_2*dt/2,t+dt/2)\); \(\vec{k}_4=\vec{f}(\vec{x}_m+\vec{k}_3*dt,t+dt)\); \(\vec{x}_{m+1}=\vec{x}_m + dt*(\vec{k}_1+2*\vec{k}_2+2*\vec{k}_3+\vec{k}_4)/6\).
Точность решения ДУ¶
Для оценки ошибок решения необходимо иметь ввиду: ошибки дискретизации (ошибки замены истинной гладкой функции на ломаную \(\approx dt\) или \(\approx dt^2\)), ошибки округления (накопление ошибок счета \(\approx dt^{-1}\)), а также устойчивость самого уравнения (см. рисунок). Уравнение может быть устойчивым (ошибки при решении не увеличиваются) или неустойчивым (все ошибки увеличиваются, часто экспоненциально). Для неустойчивых уравнений требуется тщательно выбирать метод решения и анализировать сходимость результата.
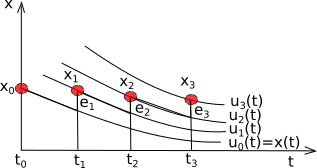
Уcтойчивая система уравнений. Полная ошибка не превосходит суммы ошибок, допущенных на каждом шаге (с точностью до постоянного множителя): \(err < \alpha(e_1+e_2+e_3+...)\).
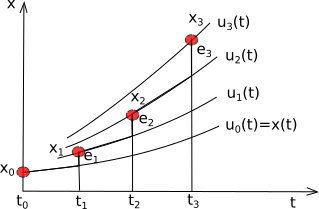
Неустойчивая система уравнений. Полная ошибка больше суммы ошибок, допущенных на каждом шаге (\(err > \alpha(e_1+e_2+e_3+...)\)) и неограниченно возрастает при продолжении решения.
Жесткие системы¶
Так же повышенного внимания при решении требуют так называемые жесткие системы. Устойчивое дифференциальное уравнение называется жестким, если оно имеет частное решение в виде убывающий экспоненты, постоянная времени которой очень мала в сравнении с длиной интервала, на котором разыскивается решение. Эта формулировка означает, что вы хотите в одной системе одновременно рассмотреть очень быстрые процессы и достаточно медленные. Причем вам интересен результат протекания медленных процессов. Быстрые процессы практически не влияют на протекание медленных, т.к. степени свободы быстрых процессов почти всегда находятся в равновесии.
Рассмотрим пример из книги Форсайта. Система:
имеет решение для начальных условий \(v(0)=u(0)=1\), которое может быть легко найдено:
Однако попытка решить такую систему методом Эйлера (или Рунге-Кутты) приводит к неприятным результатам – решение начинает расходится. Дело в том, что малейшее отклонение от истинного решения приводит систему в точку с большим значением производной. Быстро затухающая экспонента \(e^{-1000t}\) не влияет на само решение системы, но приводит к большим скачкам производной (см рисунок). Результатом этого является быстрая расходимость метода Эйлера.
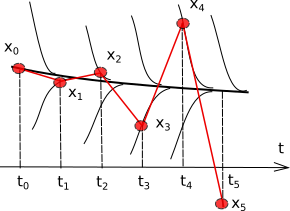
Жесткая система уравнений и явная схема. Решение неустойчиво.
Выходом их этой ситуации является использование обратного метода Эйлера или неявной схемы вычислений – использования производной для каждого шага не на левом, а на правом краю интервала: \(\vec{x}_{m+1}=\vec{x}_m+dt*\vec{f}(\vec{x}_{m+1},t)\). В таком методе производные всегда небольшие и решение является устойчивым (см. рисунок). Платить за повышение устойчивости приходится увеличением количества вычислений, т.к. для нахождения \(x_{m+1}\) в неявной схеме на каждом шаге приходится решать нелинейное уравнение \(\vec{x}_{m+1}=\vec{x}_m+dt*\vec{f}(\vec{x}_{m+1},t)\).
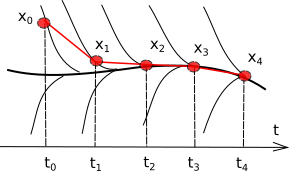
Жесткая система уравнений и неявная схема. Решение устойчиво.
Еще один пример жесткой системы - одномерное движение материальной точки в потенциале \(V(x)=C*\theta(x)\), где \(С = 10^6\). Пусть частица с энергией порядка единицы движется слева. Довольно ясно, что в область положительных х она проникнет не дальше чем 1/С, после чего упруго отразится от барьера. Поэтому можно наложить граничное условие при х=0: если при движении частицы оказалось, что х=0, х’=v>0, то нужно немедленно положить х’=-v, что соответствует абсолютно упругому удару. При попытке интегрирования уравнений движения придется выбирать очень малый шаг для получения того же результата. Это скажется на времени вычислений и на суммарной ошибке интегрирования.
Решение краевой задачи¶
В случае краевой задачи из n дополнительных условий на левом конце интервала заданы m штук: \(L_k(\vec{x}(t_0))=0, k=1...m\), и n-m условий заданы на правом конце интервала: \(R_k(\vec{x}(t_l))=0, k=1...n-m\). Для решения краевых задач ОДУ используется метод стрельбы или метод релаксации
Метод стрельбы¶
Метод стрельбы заключается в подборе недостающих параметров на левом конце интервала так, чтобы на правом конце интервала (после решения ОДУ) получилось нужное значение. Схема метода стрельбы проста:
- Введем n-m параметров \(\alpha_1,\alpha_2,...,\alpha_{n-m}\), так, чтобы получить полный набор начальных условий на левом конце \(\vec{x}(\alpha_1,\alpha_2,...,\alpha_{m-n},t_0)\), удовлетворяющих ограничениям \(L_k(\vec{x}(t_0))=0, k=1...m\);
- Решаем Задачу Коши для известных начальных значений \(\vec{x}(\alpha_1,\alpha_2,...,\alpha_{m-n},t_0)\) (выстрел) и получам значения на правом конце интервала \(\vec{x}(\alpha_1,\alpha_2,...,\alpha_{m-n},t_l)\);
- Проверяем условия на правом конце интервала \(R_k(\vec{x}(\alpha_1,\alpha_2,...,\alpha_{m-n},t_l))=0, k=1...n-m\). Если условия выполнены, то решение найдено.
- При необходимости корректируем параметры \(\alpha_1,\alpha_2,...,\alpha_{n-m}\), например методом Ньютона: \(\frac{\partial R_k}{\partial \alpha_i}=\frac{R_k(\vec{x}(\alpha_1,\alpha_2,...,\alpha_i+\epsilon,...,\alpha_{m-n},t_l))- R_k(\vec{x}(\alpha_1,\alpha_2,...,\alpha_i,...,\alpha_{m-n},t_l))}{\epsilon}\); \(\alpha_i = \alpha_i - \frac{R_k}{\partial R_k/\partial \alpha_i}\) Таким образом на каждую итерацию необходимо n-m+1 решений задачи Коши.
Несколько замечаний по методу стрельбы:
- Eсли больше условий задано на правом конце интервала m < n-m , задачу Коши решаем в противоположную сторону (если это возможно).
- Возможны ситуации с неравнозначностью движения по траектории в разные стороны, например для уравнения теплопроводности.
- Возможны ситуации, когда сшивать решения нужно в середине интервала, например при решении уравнения Шредингера.
Релаксационные методы¶
Релаксационные методы основаны на формировании системы уравнений для значений функции \(\vec{x}(t_k)\) в узлах сетки. Система уравнений, для этих значений имеет вид: \(\frac{\vec{x}(t_{k+1})-\vec{x}(t_{k})}{dt}-\frac{\vec{f}(x(t_{k+1}))-\vec{f}(x(t_{k}))}{2}=0, k=0...l\); \(L_k(\vec{x}(t_0))=0, k=1...m\); \(R_k(\vec{x}(t_l))=0, k=1...n-m\).
Остается решить полученную систему.