Методы Монте-Карло

Получение и проверка случайных чисел

При работе со случайными числами обычно используют последовательности чисел каждое из которых лежит в полуинтервале [0,1). Случайность заключается в том. что следующее число абсолютно не зависит от предыдущих.

  • Таблицы случайных чисел использовались когда отсутствовали надежные методы получения случайных чисел. Например таблица чисел, полученная на рулетке могла использоваться для компьютерного моделирования. Преимущество - быстрота, недостатки - конечный размер, большой объем памяти.
  • Датчики случайных чисел использовались когда часть функций в компьютере было проще реализовать аппаратно (при помощи дополнительного устройства). Сейчас практически не используются.
  • Псевдослучайные числа - самый распространенный способ получения случайных чисел. Недостаток - неслучайность (существование некоторых закономерностей, которые, впрочем, трудно найти). Реализуются в виде случайных последовательностей. Примеры случайных последовательностей: \(\xi_0=0.1; \xi_{i+1}=\{\pi*\xi_i\}\) или \(\xi_0=2^{-m}; \xi_{i+1}=\{M*\xi_i\}\), где m -порядка машинного нуля, а M - порядка самого большого числа в ЭВМ.

Проверка случайных чисел заключается в обнаружении корреляций разного сорта в элементах случайной последовательности.

  • Проверка частот - частота различных цифр в таблице.
  • Проверка пар - частота различных двухзначных пар.
  • Проверка серий - количество повторов.
  • и т.д.
Простой пример тестирования набора случайных данных для проверки частот (запустить)
#!/usr/bin/python 
""" simple test for uniform random distribution
"""
import pylab as py
from random import random

N = 10000
Nbins =100
x1 = [random() for i in range(N)]
py.hist(x1, Nbins, normed=1., facecolor='g', alpha=1.)
py.title('Number of points = %i, number of bins = %i' % (N,Nbins))
py.grid(True)
py.show()

Обратите внимание на то, сколько испытаний нужно провести для получения равномерного плотного распределения с небольшими отклонениями.

Получение и преобразование случайных величин

Метод обратной функции

Случайная величина \(\eta\) характеризуются функцией распределения F(x) такой, что \(P\{\eta < x \} = F(x)\). Альтернативно можно использовать плотность вероятности f(x), определяющую вероятность попадания значения \(\eta\) в интервал x…x+dx: \(f(x)*dx = P\{ x < \eta < x+dx\}\). Легко проверить, что \(F(x)=\int_{-\infty}^x f(x)dx\).

Для построения случайной величины с заданным распределением в качестве исходных данных обычно используется последовательность случайных чисел из полуинтервала [0,1), или, что то же самое, случайная величина \(\gamma\) с равномернымраспределением на интервале 0-1.

В методе обратной функции используется то, что величина \(\xi=F^{-1}(\gamma)\), где \(\gamma\) - величина равномерно распределенная на полуинтервале [0,1), имеет функцию распределения F(x) [1].

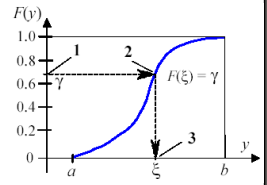
../_images/mc_revers.png

Если функция распределения и обратная функция может быть записана аналитически, то не сложно построить величину с требуемым распределением:

  • Равномерно распределенная величина на полуинтервале [a,b): \(\int_a^{\xi}\frac{dx}{b-a}=\frac{\xi-a}{b-a}=\gamma\) отсюда получаем \(\xi=a+(b-a)*\gamma\).
  • Распределение Пуассона: \(\int_0^{\xi} \lambda e^{-\lambda x}dx=1-e^{-\lambda \xi}=\gamma\) отсюда получаем \(\xi =-\frac{1}{\lambda}ln(1-\gamma)\).

Метод исключения

Рассмотрим фунцию плотности вероятности f(x) на некотором интервале (a,b). При этом условимся, что плотность вероятности не превосходит значения М. Зададим пару случайных величин \(\gamma_1, \gamma_2\) таких, что \(\gamma_1\) имеет равномерное распределение на интервале (a,b), а \(\gamma_2\) - равномерное на интервале (0,M). Если \(\gamma_2 < f(\gamma_1)\), то используем \(\xi = \gamma_1\), в противном случае выбираем другие точки.

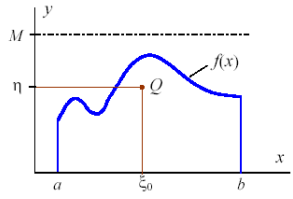
../_images/mc_elimin.png

Можно заметиить, что такая процедура дает случайные числа из интервала (a, b) причем их плотность больше, если f(x) принимает большие значения (меньше точек отбрасывается). Данный алгоритм -универсален, однако влечет большое количество накладных расходов: каждый раз используется пара случайных чисел вместо одного, много точек может быть отброшено, т.е. часть времени тратится впустую.

Многомерные случайные величины Последовательное моделирование координат Метод замены переменных

Вычисление интегралов методом Монте-Карло

  • Метод простого Монте-Карло

Известно, что интеграл от функции равен среднему значению функции умноженному на интервал интегрирования:

\[M\{f(\xi)\}=\int_a^b f(x)p_{\xi}(x)dx=\frac{1}{b-a} \int_a^b f(x) dx.\]
../_images/mc_simple.png

Отсюда можно получить значение интеграла, если найти среднее значение функции:

\[\int_a^b f(x) dx = (b-a) M\{f(\xi)\} \approx (b-a) \bar{f(\xi)}_N = \frac{b-a}{N}\sum_{i=1}^{N} f(\xi_i).\]

Получается, что нужно посчитать значение функции в большом числе случайных точек (равномерно распределенных по интервалу интегрирования) и найти их среднне.

  • Геометрический метод Монте-Карло

Пусть требуется вычислить интеграл \(\int_a^b f(x)dx\) и известно, что функция положительна и ограничена сверху значением M. Задаем пары случайных величин \(\xi,\) - равномерная на итервале (a,b), \(\eta\) - равномерная на интервале (0,М). Из N пар находим удовлетворяющие условию \(f(\xi)<\eta\), т.е лежащие под графиком функции.

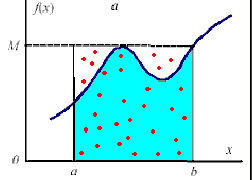
../_images/mc_geom.png

Значение интеграла равно площади под графиком функции: \(\int_a^b f(x)dx \approx M*(b-a)\frac{K}{N}\), где K - число точек лежащих ниже графика функции.

  • Оценка ошибки
  • Построение доверительного интервала в случае большого числа испытаний, когда дисперсия известна.

Центральная предельная теорема утверждает, что вероятность отклонение значения случайной величины a от среднего значения \(\bar{\xi}_N = \frac{1}{N}\sum_{i=1}^N \xi_i\), вычисленного по N испытаниям равна интегралу ошибок:

\[P\{|\bar{\xi}_N-a|< x \sqrt{\frac{D_{\xi}}{N}}\} \approx \sqrt{\frac{2}{\pi}} \int_0^x e^{-t^2/2}dt,\]

где x - параметр, определяющий доверительный интервал.

Дисперсию можно оценить по тем же N испытаниям \(D_{\xi} = \frac{1}{N}\sum_{i=1}^N \xi_i^2 - (\frac{1}{N}\sum_{i=1}^N \xi_i)^2\). Стоит оговориться, что использование данной оценки для дисперсии не является математически строгим.

Таким образом необходимо задать допустимую доверительную вероятность \(\beta\) и найти параметр x из уравнения \(\sqrt{\frac{2}{\pi}} \int_0^x e^{-t^2/2}dt = \beta\). Доверительный интервал равен \(x \sqrt{\frac{D_{\xi}}{N}}\). Таким образом доверительный интервал (при заданной вероятности) уменьшается обратно пропорционально корню из N, что очень медленно. Поэтому методы Монте-Корло применяют только для оценки интегралов, в основном – многомерных.

  • Повышение точности

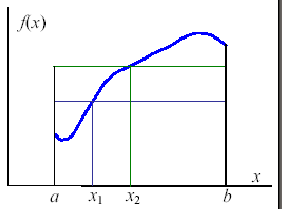
Основа повышения точности вычислений по методу Монте-Карло заключается в уменьшении дисперсии каждого измерения \(D_{\xi}\). Этого можно добится сужая интервал в котором изменяется функция. Первый способ заключается в разбиении области интегрирования на части, в которых границы изменения функции уже. Второй способ - выделение главной части подынтегральной функции. Для этого из подынтегральной функции вычитают близкую функцию, интеграл от которой известен. Полученная разность хорошо интегрируется методом Монте-Карло, т.к. имеет малое отклонение от нуля.

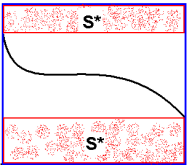
../_images/mc_pres.png

Повышение точности уточнением пределов (S* не учитывается)

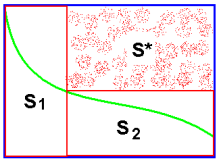
../_images/mc_pres1.png

Повышение точности разбиением интервала (S* не учитывается)

[1]Соболь И.М. Численные методы Монте-Карло. М:Наука 1973, 312с.